Minimum spanning tree in a graph

What is a minimum spanning tree, what is minimum in it

Minimum spanning tree is a tree which is a subgraph , with a MINIMUM total edges in a subgraph. If this is a weighted graph the edges needs to be minimum cost edges/minimum weight edges.

CUT Property in graph Cut is a partition of vertices in a graph in two disjoint subsets In figure

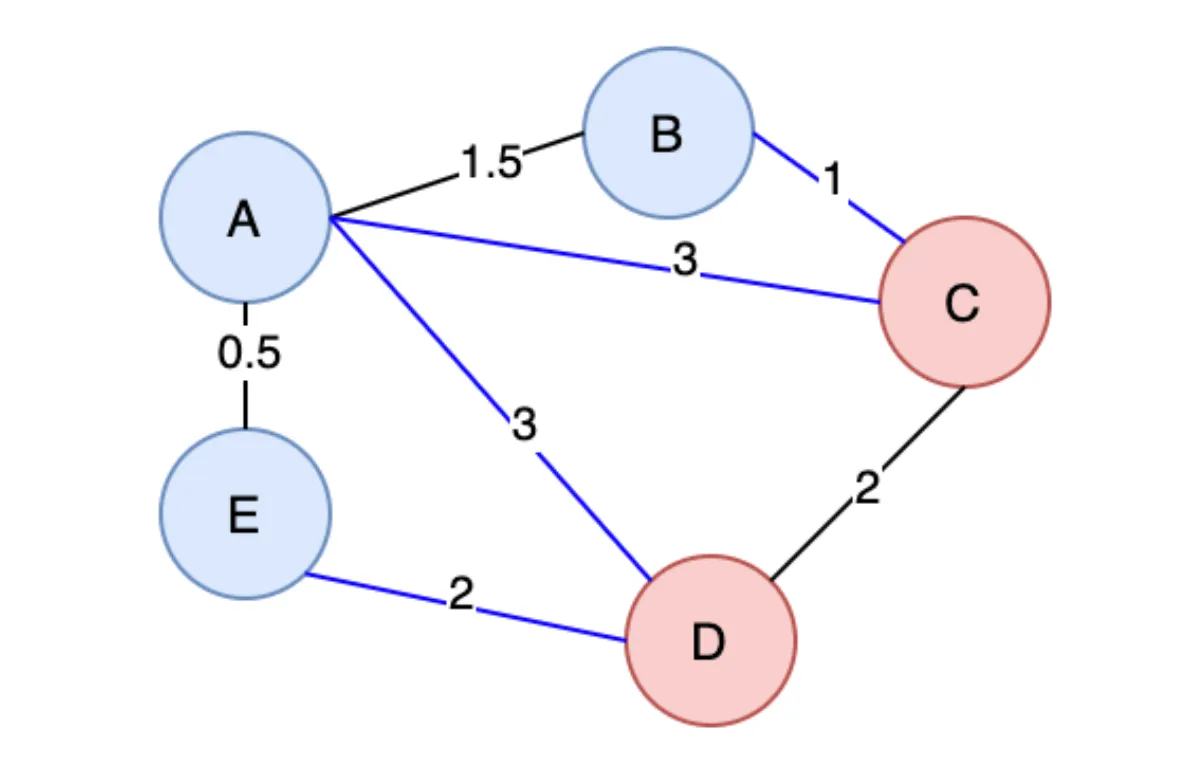
There are two disjoint sets : [E, A, B] [C, D] A crossing edge is an edge that connects vertices of one edge with another edge of disjoint sets example : (A, C) (A, D) (B, C) (E, D) are all crossing edge

Cut of a graph : For a cut C in a graph, if the weight of an edge E in cut set of a C is strictly smaller than any of the other weighted edges of the cut set of C, then edge belongs to minimum spanning tree of the graph

Now, 2 good questions here.

1. Are there really a need for 1 edge ? why cant there be 2 edges ?
2. Why is there a need for edge with minimum weight only?

Ans1. If there is more than 1 connecting edge, then it is definite to form a CYCLE and remember we are talking about minimum spanning TREE requirement is to connect all vertices with fewest edges Ans2. the edge with least weight would be needed to construct minimum spanning tree