Given points minimum cost to connect all points

Given points print minimum cost to connect all points

The cost is manhattan diatance between them |xi-xj| + |yi-yj| Points are connected if there is exactly one path to connect them

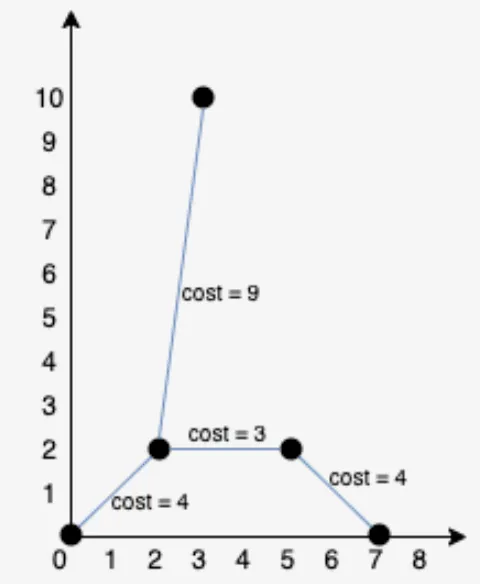
Conditions for Kruskal Algorithm

1. Ascending order sorting of the edges
2. Start choosing edges based on above output, to form minimum spanning tree, skip the edges that produce cycles
3. Repeat step 2 until the n-1 edges are formed

int rank[];
     int root[];
     public static void main (String args[]) {
        MinimumCostToConnectAllPoints minCost = new MinimumCostToConnectAllPoints();
        int[][] points = {{0,0},{2,2},{3,10},{5,2},{7,0}};
        minCost.minimumCostToConnectAllPoints(points);
    }

    
    private int minimumCostToConnectAllPoints(int [][] points) {
       //use union find to find if they are already connected, add their weight, if they return false they are already connected
       //use condition to find less than n-1 edges needs to be connected
       root = new int[points.length];
       rank = new int[points.length];
       for (int i =0; i < points.length; i++) {
          root[i] = 0;
          rank[i] = 0;
       }

       ArrayList<int[]> allEdges = new ArrayList<>();

       //step1: store all the edges as a graph
       for (int point1 = 0; point1 < points.length; point1++) {
          for (int point2 = point1+1 ; point2 < points.length ; point2++) {
              
              int weight = Math.abs(points[point1][0]-points[point2][0])+ Math.abs(points[point1][1]-points[1][1]);  
              System.out.println("Point (" + point1 + "," + point2 + " )" + " weight " + weight);
              int[] edge = {weight, point1, point2}; //points here refer to the index
              allEdges.add(edge);
          }
       }

       Collections.sort(allEdges, (a, b)-> Integer.compare(a[0], b[0]));
       int edgesUsed =0;
       int mstCost =0;
       //do union find by Rank
       for (int i=0; i< allEdges.size() && edgesUsed < points.length-1 ; i++) {
            
        int point1 = allEdges.get(i)[1];
        int point2 = allEdges.get(i)[2];
        int weight = allEdges.get(i)[0];
        if(union(point1, point2)){
            System.out.println("These edges arent connected before hence adding their cost " + point1 + "  " + point2);
            mstCost += weight;
            edgesUsed++;
        }
       }
       return edgesUsed;
    }

    private boolean union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);

        if(rootX == rootY) {
            return false;
        } else {
            if(rank[rootX] > rank[rootY]){
                root[rootY] = rootX;
            } else if(rank[rootY] > rank[rootX]) {
                root[rootX] = rootY;
            } else {
                root[rootY] = rootX;
                rank[rootX] =+ 1;
            }
        }

        return true;
    }

    private int find(int x) {
        if(root[x] != x) {
           root[x] = find(root[x]);
        }
       return root[x];
    }